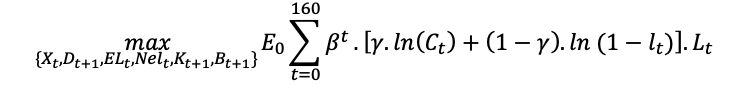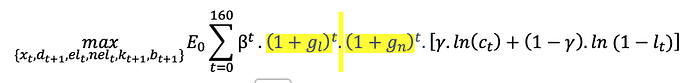DSGE model in efficiency units

General DSGE Modeling
1

Good morning everyone,

If I want to express the utility function per efficiency units of labor, is the new discount rate the following: beta.(1+n)(1+a) ? (n) being the growth rate of population and (a) the growth rate of labor technical progress, assuming that L(t)=(1+n).L(0), and A(t)=(1+a).A(0).

Besides, I often see in papers that all variables expressed in per capita terms are divided by the same L(t). My issue is that very often, that L(t) is expressed as the population. But why do they divide the consumption and the labor factor, for example, by the same L(t)? I find it odd since I would divide both by total employed persons, since they are the ones making consumption decisions and labor supply decisions. Or maybe most papers mistake “population” by the “workforce”.

Thank you in advance.

Best,

2

Hi dacorb,

  1. The discount rate is a deep parameter in the model, not a variable. It does not need to be rescaled.

  2. If you do not have a model with unemployment, individuals in standard DSGE models make a decision at the intensive margin, but not at the extensive margin. So every member of the household works, but decides how many hours of labour to supply, not whether or not to supply hours of work.
    In this sense, the concepts of population and workforce coincide in such models.
    :slightly_smiling_face:

3

Thank you for your clear response.

  1. My issue is rather with the utility function. If I want to express everything in per efficiency unit of labor, I have to incorporate in the household’s program the two growth rate somewhere.

The utility function in level is:

36
Capture d’écran 2019-07-05 à 09.30.36.png733×91 5.09 KB

The utility function per efficient worker should be (?):
45
Capture d’écran 2019-07-05 à 09.37.45.png872×106 12.3 KB

g(n) being the growth rate of the population and g(l) the growth rate of the technology.

  1. Ok that’s very clear. My issue now is for the data. If I enter the model in per efficient labor units, I have to divide all my time series by either population or workforce. My issue with the workforce is that it does not take into account the consumption of retired people. Well, it is actually taken into account but at the level of the household. Since I do not model an OLG model, I guess this is not really a problem. I would end up with an average consumption per " efficient worker" higher than what is observed.

Thanks again for the clarification

4

Point 1 of @cmarch is not complete. The discount factor \beta itself is a structural parameter. But if you start with a model including a growth trend, then you need to detrend it and work with a growth-adjusted discount factor \tilde \beta. With log utility, the g_n should drop out as it leads to additive separability.
\beta^t \log(C_t)=\beta^t \log(c_t(1+g_n)^t)=\beta^t \log(c_t)+\beta^t t\log(1+g_n)
When taking the derivative, the latter part will always drop out.

1 Like
5

Oups yes I forgot the logs. That’s what I had in mind. Thank you !