Another estimation query

Estimation ML/Bayesian estimation
1

Trying to estimate the log-linear version of Ascari, Sbordone, Macroeconomics of trend inflation (2013). This is a standard Keynesian model, but with non-zero steady state inflation. So the only thing different in this estimation from baseline models would be the treatment of inflation. In this case, should I use first difference inflation as an observable? The code I am working with can be found on sites.google.com/site/pfeiferecon/dynare
(Replication file for Ascari/Sbordone (2014): “The Macroeconomics of Trend Inflation”, Journal of Economic Literature, 52(3), pp. 679-739. It shows i) how to map steady state relations inside of a mod-file based on a nonlinear model and ii) how to manually map the determinacy and stability region: AscariSbordone2014.mod (requires the Dynare unstable version))

2

With inflation, we almost never work with first differences. Inflation itself is already a first difference of the CPI or the GDP deflator.
You should just use the level of net or gross inflation as the observable. But as you are interested in the mean, you should not demean inflation.

3

Thank you for the comments. Let me explain:

  1. I have three variables that can be observed, output gap, inflation and interest rate
  2. Output gap and interest rate rate are deviations, so I have used HP filtered growth for GDP, and HP filtered interest rate
  3. Now inflation is in logs in this model. Small pi = log(PI). So in the dynare code the authors write pi in gross terms. I use the following transformation --> y = log(GDP_def_t/GDP_def_t-1) and pi_obs = y^4 (y to the power 4). Here GDP_def_t is gap deflator at time t.
  4. Lets say I want to estimate ‘steady state’ inflation, log(pi). Then can I directly estimate it like I have done? (code + data attached)
  5. If 4 is correct, then the value I am getting for log(pi) is very different from the data. I am assuming that is a model specification issue rather than a code issue. As before, I am using the code from your page.
    data_us.xls (56.9 KB)
    lina.mod (3.27 KB)
4
  1. That’s Zombie economics that never dies, regardless how often I tell users: Never use an HP filter for detrending data for estimating a DSGE model!!! (See my Guide to Observation Equations for details)
  2. I am not following your description. If pi = log(PI) then PI was a gross inflation rate and pi is a net inflation rate.
5

Once again, thank you for replying.

  1. I am using HP filter based on this paper: Estimating the Evolution of Money’s Role in the U.S. Monetary Business Cycle, JMCB 2012.

  2. sorry about the confusion, pi = gross inflation. Is it possible to estimate this in the data like I am doing? Any way I can check my results?

6
  1. Despite the paper you cite, I still consider HP filtering your data to be plain wrong for estimating DSGE models
  2. Your observation equation is
inflgdpq = pi + constepinf;

with

constepinf=log(ti); % inflationtarget

This is an observation equation for a non-mean 0 net inflation rate. But your excel file stores the gross inflation rate in inflgdpq. In this case, you should have the observation equation

log(inflgdpq) = pi + constepinf;

which states that the logarithm of the gross inflation rate stored in inflgdpq, which is the net inflation rate, is matched to the net interest rate including the inflation target in the model.

7

Also in your paper, “A Guide to Specifying Observation Equations for the Estimation of DSGE Models”, you mention that “For some models, it is useful to work with the net inflation rate instead of gross inflation rate”. But you didn’t discuss which kinds of models one should use net or gross inflation rate. It seems
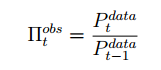Screenshot from 2021-12-08 11-50-50 for non-linear model
and
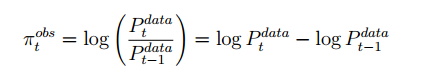Screenshot from 2021-12-08 11-50-59 for a log-linearized model.

Yeah? Or there is more…to that statement. Thanks!

8

Yes, for linearized models, it’s typically the net inflation rate.

1 Like